УЧЕТ ИСКАЖЕНИЯ ИНФОРМАЦИИ В ЗАДАЧАХ НАВЕДЕНИЯ

Как показано в третьей главе, оптимальное управле­ние является безынерционной функцией текущей оценки

фазовых координат объекта x(t), на основе измеренных значений вектора г.

Когда наблюдаемый вектор z определяется выраже­нием

z(t)=Cx(t)—n{t), (5.117)

где С — прямоугольная матрица (ІХп), являющаяся из­вестной функцией времени; n(t) —вектор белых шумов с уровнем N (t); x(t) — вектор фазовых координат линей — ного объекта, оденки фазовых координат определяются уравнениями:

Ax{t)+Bu + R{t)CTN~’ [z{t) — Cx(t), (5.118) x(to)=Mx0i

A£-=AR + RAT-RCTN-‘CR-{-$(t), (5.119)

В системах телеуправления информация о текущих значениях вектора x(t) может искажаться це*>ю, созда­ющей помехи. В связи с этим изменяется и зависимость

текущей оценки x(t) от вектора z(t). Задача учета иска­жений информации при приеме сводится к получению

выражений, связывающих x(t) с z(t) в случаях, когда связь z (t) с x(t) отличается от условия (5.117).

Предположим в общем случае, что наблюдаемый вектор z(t) определяется выражением

z{t)=y{t)+n{t ] (5.120)

где вектор y(t) случайно связан с вектором фазовых ко­ординат x(t) объекта управления. Пусть известен услов­ный закон распределения у (і) при заданном *(0. Р(у1х), который не зависит от прошлой информации z(x),x<t и имеет конечные первый и второй моменты. В этом случае по формуле условных вероятностей имеем

Р(г,1х,)=§ PiZtlyJPiyt/xJdy,. (5.121)

sy

Если n(t) подчиняется нормальному закону распре­деления с нулевым математическим ожиданием, то для момента имеем

Разложим выражение (5.122) в ряд по At—U — и подставим его в равенство (5.121). При конечных пер­вом и втором моментах

5 УіРІУіІхі)аУі=Мхі)> (5.123)

ЯУ

Г yi!/ip{yi/xi)dy,=^%(xt) (5.124)

выражение (5.121) может быть представлено в виде

где 0 {At) означает члены более высокого по сравнению с At порядка малости.

Получим для этого случая уравнение, определяющее апостериорный закон распределения фазовых координат объекта x(ti) при наблюдении вектора г на интервале (/о, ti), где і принимает целые значения.

Обозначая через

Pi(*t)=.P(*il* о) (5.126)

апостериорный закон распределения x(ti) при наблюде­ниях г на интервале {to, U) и через

Я,_і(*,_і)=/>(*,-іДггі-1) (5.127)

этот закон распределения на предыдущем шаге. По фор­муле Байеса получим

Pi i. Xl) = kiP (zJXi, 2o~l) J P(Xi/X,-U zt’ix

8 (■»/-!)

XPi-x(.Xi-x)dxt-r, (5.128)

где ki — коэффициент нормировки;

Q (лгг—і)—область возможных значений векто­ра x{ti-1).

На основании предположения о независимости услов­ного знакона Уі от прошлых наблюдений и некоррелиро­ванности значений шума n(ti) в разные моменты време­ни, получаем _

P(*i/x„ Zb~l)=P(*ilxt). (5.129)

Рассмотрим случай линейного объекта управления х=Ах—Ви, x(i0)=x0. (5.130) Для дискретного случая при малых At=U-x —1{, мож­но записать Xi — Xi-i-l-AxiM-^Bui-iM. (5.131) Поэтому условный закон распределения Р (Xi/xi-u Zo-1)=8 (Л*/—1 — (Е — АAt) Xt + Ви 1-хAt), (5.132) где б—дельта-функция Дирака; Е — единичная матрица. Подставляя выражения (5.129) и (5.132) в формулу (5.128), получим Pi(xl)=klP(zi/xl)Pi-x{[E—Akt]xt—Bui-xM). (5.133) Для получения дифференциального уравнения пред­положим Р{—х дифференцируемой функцией аргумента, имеющей непрерывные производные до второго порядка, и разложим ее в ряд Тейлора, ограничившись величина­ми — порядка At. Получим Р 1-і ([£ — A At] Х[ — Bui-At) = Pi-i {xt) — дРх-х (*г)

 

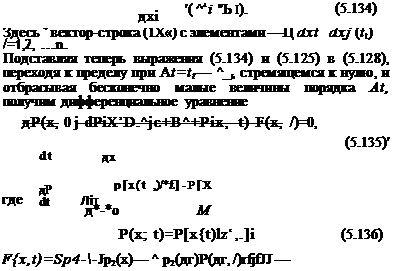Sp — след матрицы, р,] и рг определяются выраже­ниями (5.123) и (5.124); N — уровень белого шума n(t).

В качестве начального условия в уравнении (5.135) используется априорный закон распределения фазовых координатх в момент t0, равный Р(х0). Уравнение (5.135) может быть решено в общем виде с помощью обычного метода характеристик, применяемого для дифференци­альных уравнений в частных производных первого по­рядка.

Из уравнения (5.130) следует

х (t0)=kT(f, t0)x(t)— f kT(xt Q 4u{x)dx, (5.137)

*0

гpekT(t, t0) —импульсная переходная матрица системы сопряженной (5.130). Поэтому

Р(х, /)=P0|V(<, і0)х(і)—^кт{х, t0)Bu{x)dx, X X exp I — I* [kT (t, x) x (t) — (5.138)

l to

— j kT ((*., т) Чи (p) flip, t] dtI,

где Po — априорный закон распределения Xo в момент to — Подынтегральное выражение в показателе экспоненци­альной функции является результатом замены в форму­ле (5.136) функции х(т) в pi и р2 их выражениями при А)=т. Поскольку в выражение (5.136) входят средние значения искомого распределения, окончательное реше­ние может быть получено после определения

Мг= f РіДО/Ч*. t)dx, (5.139)

•/W2=f р2(х) Р (х, t)dx (5.140)

К

и решения алгебраической системы уравнений относи­тельно Мі и М%. Зная Р(х, t), апостериорное математи­

ческое ожидание фазовой координаты объекта x(t) мож­но определить из выражения

x(t)=j хР(х, t)dx. (5.141)

Полученные выражения дают принципиальную воз­можность решения задачи оптимального управления при действии мультипликативных помех, однако фактическое получение решения сопряжено с вычислительными труд­ностями.

Рассмотрим возможность применения уравнения (5.135) к задачам управления при действии помех.

Предположим, что цель имеет возможность создавать помехи, исключающие прием полезного сигнала x(t) на­водящимся объектом на некоторых интервалах внутри (*о, *»). Такое положение имеет место, когда происходит прекращение поступления информации о положении це­ли вследствие действия помех [22].

Если принять, что срывы сопровождения происходят в известные моменты времени, то решение может быть получено приравниванием к нулю элементов матрицы С в (5.118) и (5.119) на интервалах прекращения сопро­вождения. В частности, если

С (<)=0 <*</«, (5.142)

то из выражений (5.118) и (5.119) следует, что на этом интервале

—= АхЛ)+Ви (5.143)

dt

-=AR-YRAr+S(t) (5.144)

dt

при заданцых^лг^^и R (/J.

Уравнения (5.143) и (5.144) соответствуют априор­ным оценкам вектора *(г).при отсутствии наблюдений. Таким образом, если матрица С(^)=0, то обработка ин­формации в системе наведения эквивалентна прекраще­нию приема вектора г и переходу к априорным оценкам фазовых координат объекта. При этом в качестве на­чальных значений принимают оценки, имевшие место в последний момент получения информации.

. Заметим, что подобный результат имеет место также в случае, когда уровень белого шума л(^), равный N, неограниченно возрастает.

Фактически в системе наведения осуществляется при этом пролонгация координат цели на основе априорной гипотезы о ее движении.

Другим предельным случаем является представление элементов матрицы С в виде случайных процессов, зна­чения которых в разные моменты времени независимы и равны 0 с вероятностью и единице с вероятностью 1 —Яі-

В этом случае вектор z может быть представлен в виде

z=Cax—n(t), у(х)=Сах, (5.145)

где a(t) диагональная матрица (пХп) с0 Случайны­ми элементами а, ц (/), подчиняющимися закону распре­деления с плотностью:

P>jj (О=Яі {t) § l*J} (t)] + [ 1 — qj (t)] 8 [ajj (t)- I], (5.146)

где 6[ajj] — дельта-функция. Если кроме того, считать ajj (t) независимыми для разных / в один и тот же мо­мент, то совместный закон распределения а(/) равен произведению законов распределения каждого элемен­та и

^«(0=П^(0- (5.147)

i-i

Положим для простоты а (і) скалярной функцией, что соответствует одновременному обращению в нуль всех элементов векторах^) с вероятностью q(t). В этом слу­чае в уравнении (5.135) функция (5.136) может быть за­писана в виде

F (х, t)=SpA + Я-=±- [xTCTN~’Сх-Sp(CTN~’С X

X Dx (*))]-(1 — q)(x-xYCTN-‘z. (5.148)

Сравним равенство (5.148) с выражением функции

р(х, t) при неслучайной матрице С, которое имеет место при

Яс(С)=8(С-Сх) (5.149)

Fc (х, t)=SpA +-І — [xTClN-VCjX — — Sp(ClTV"1 C1PX{t)-Lx-xJCx N~’z. (5.150)

Отсюда следует, что выражение (5.148) и (5.150) сов­падают, если в формуле (5.150) уровень ошибок измере­ний увеличить в 1/1 — q раз.

Поскольку математическое ожидание и дисперсионная матрица x(t), соответствующие формуле (5.150), удовле­творяют уравнениям (5.118) и (5.119), оценка текущих фазовых координат х в условиях, когда полезная инфор­мация в наблюдаемом векторе z(t) становится равной нулю с вероятностью q(t) независимо от прошлых мо­ментов времени, удовлетворяет уравнению

-£-= Лх(/)+*#(i) + R (/)CTN~X (1 — q)[z{t)-Cx(*)].

at

(5.151)

При этом

— = AR—RAT-RCTN~'(l-q)CR. (5.152)

dt

Таким образом, в рассматриваемом случае оценка *(£) сводится к оценке без потери информации при уве­личении уровня N белого шума ошибок измерений в 1/1 — q раз.

Рассмотрим также случай, когда

(5.153)

где С — случайная матрица с известным законом распре-
деления Рс(с), в общем случае зависящим от времени.
В этом случае функции р(х, і) (5.136) примет вид

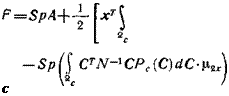CTN~xCPc (C)dC-x-

-{x-xf CTPc{C)dC-N~’z. (5.154)

Р2х= I" ххтР(х, t)dx (5. 155)

V

= хР(х, t)dx (5. 156)

Пс, Q* — области возможных значений x(t) и С.

Будем искать в этом случае решение (5.135) в виде

Р(х, t)=kexр—l-[(x-x)TD~1 (лг-jc)]. (5.157)

Подставляя выражения (5.157) и (5.136) в (5.135) и приравнивая коэффициенты при степенях х нулю, по­лучим

= Ах + Ви + D ^ СтРс (С) dCN~l z —

— j CTN~’CPc{C)dC-x) (5.158)

и D=AD + DAT-D j CTN~’CPc{C)dC-D. (5.159)

Из сравнения этих выражений с формулами (5.118) и (5.119) следует, что если матрица С случайна с извест­ным законом распределения Рс, то оценки текущих коор­динат объекта совпадают с оценками для детерминиро­ванной матрицы С при замене С и CTN~lC математиче­скими ожиданиями.

1.